How Python manages and represents integers of arbitrary size

Understanding Unbounded Integer Precision in CPython: An In-Depth Exploration

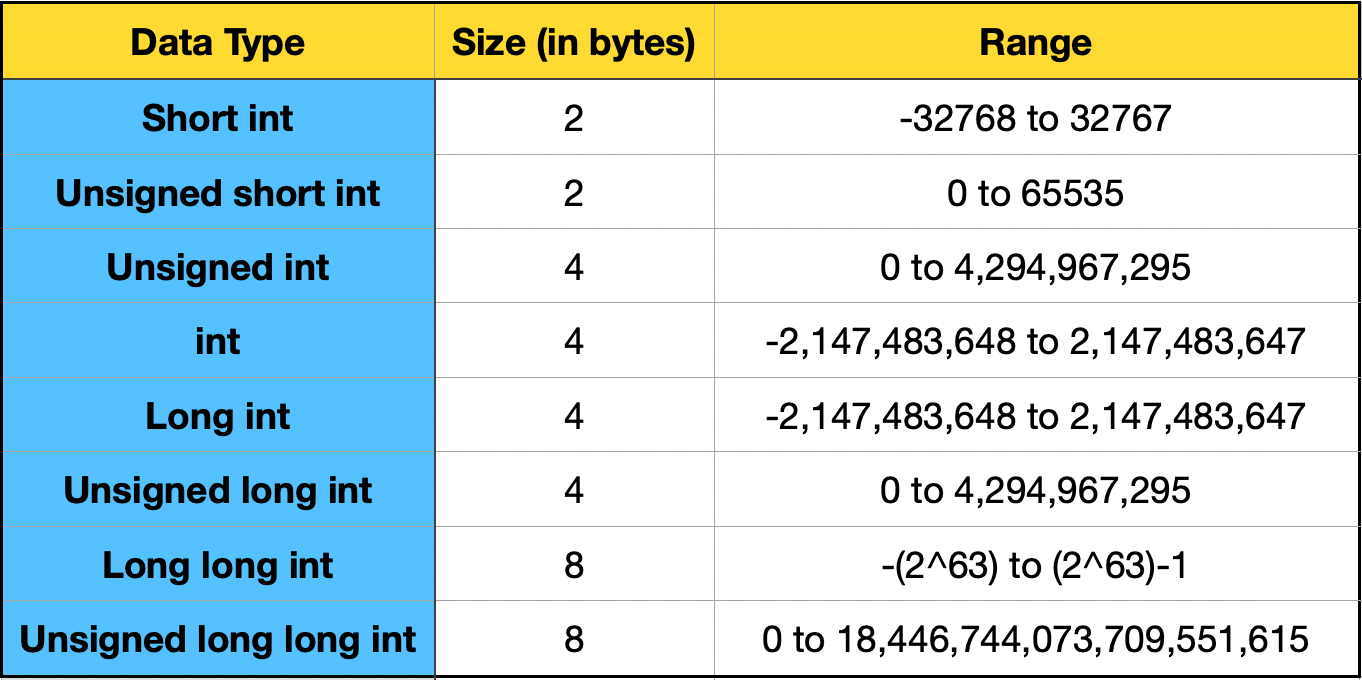
In C/C++, we have three different data types for storing integers, depending on the size of the integer to be stored. These are:

Therefore, when coding in C/C++, one must carefully choose the appropriate data type to store an integer based on its size. However, this is not an issue in Python, as Python can handle arbitrarily large numbers limited only by the available memory of the system.

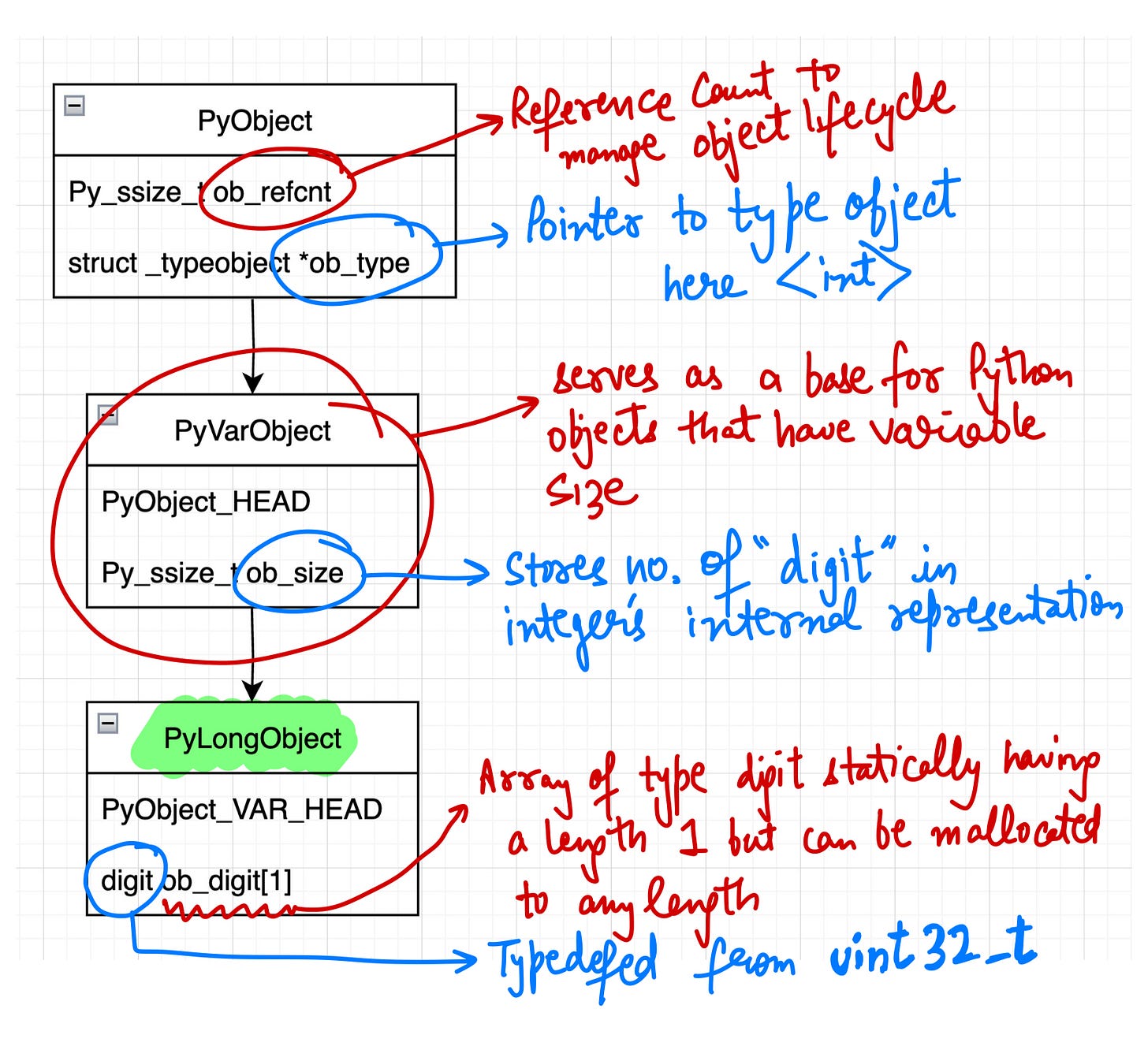
If you define an integer in Python, internally it creates an object of type PyLongObject. It looks like:

struct _longobject {
    PyObject_VAR_HEAD 
    digit ob_digit[1];
};

• ob_digit is an array of type digit which statically is having a length 1. However, if required it can be mallocated any length as it is a pointer to a digit.

• The digit datatype is typedef’ed from uint32_t.

• PyObject_VAR_HEAD is a macro used in CPython to define the header of variable-sized Python objects. It opens up to :

typedef struct {
    PyObject_HEAD
    Py_ssize_t ob_size;  // Length of the variable-size object
} PyVarObject;

• ob_size contains the length of variable sized object i.e. the count of elements in the array ob_digit in case of PyLongObject.

• PyObject_HEAD is a macro that contains a reference count and a pointer to the type object. This also opens up to :

typedef struct {
    Py_ssize_t ob_refcnt;  // Reference count
    struct _typeobject *ob_type;  // Pointer to the type object
} PyObject;

Overall the picture looks like:

▶️ How are very large integers stored in Python?

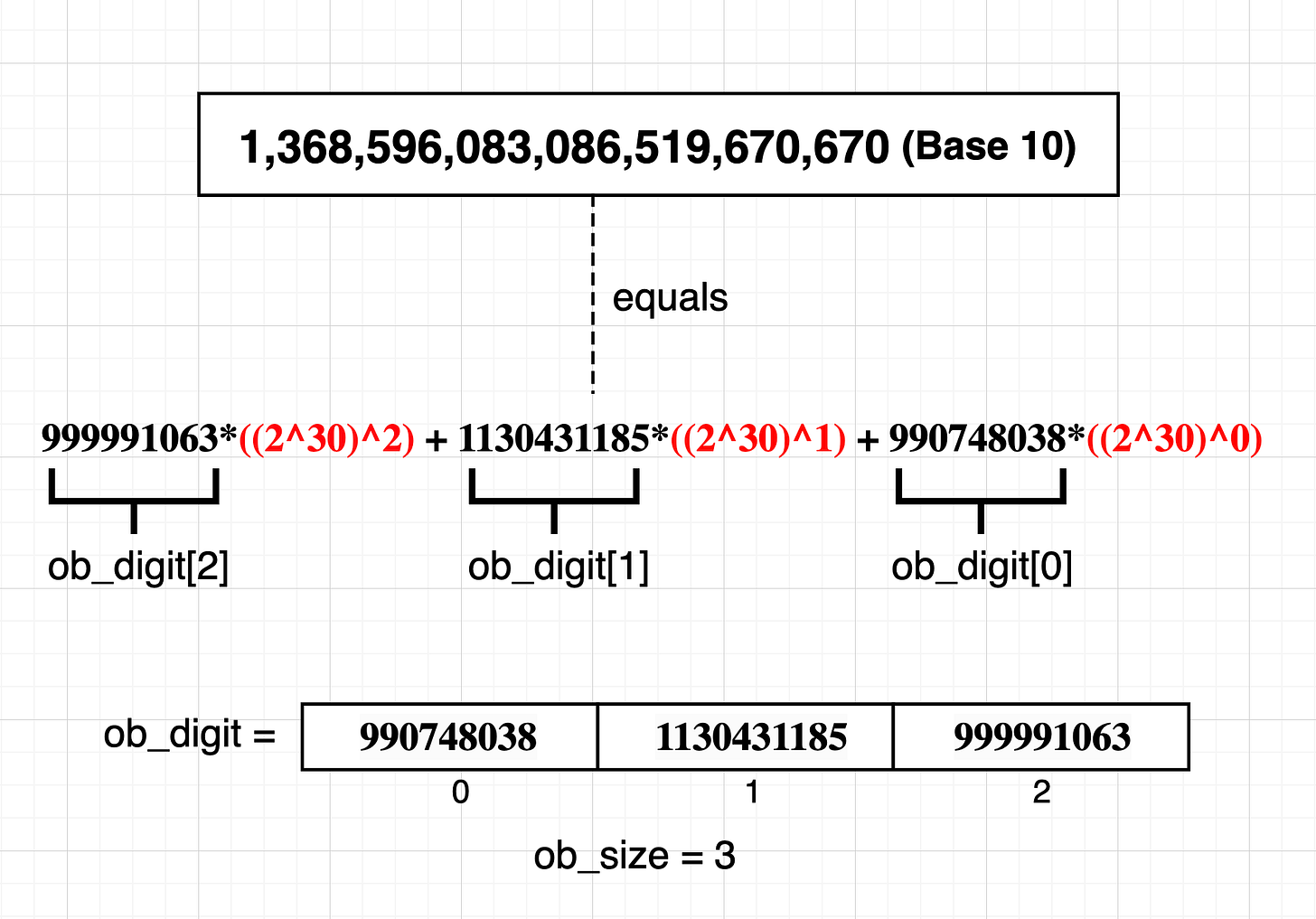
Now, ob_digit is an array of digit and each digit is typedef’ed from uint32_t due to which each digit can store a value from 0 to 2^32-1. Thus, the algorithm becomes :

1. Convert the integer to be stored from base 10 to base 2^30.

2. Store each element we get by converting the integer to base 2^30 as a digit.

3. The number of elements becomes the value of ob_size.

In this way, Python efficiently utilises nearly all of the 32-bit space allocated per digit. This approach helps maintain resource efficiency and allows Python to perform operations like addition and subtraction with simplicity, similar to grade-school arithmetic.

🙋🏻‍♂️ Why do we convert the integers from base 10 to base^30 (why not directly store them)?

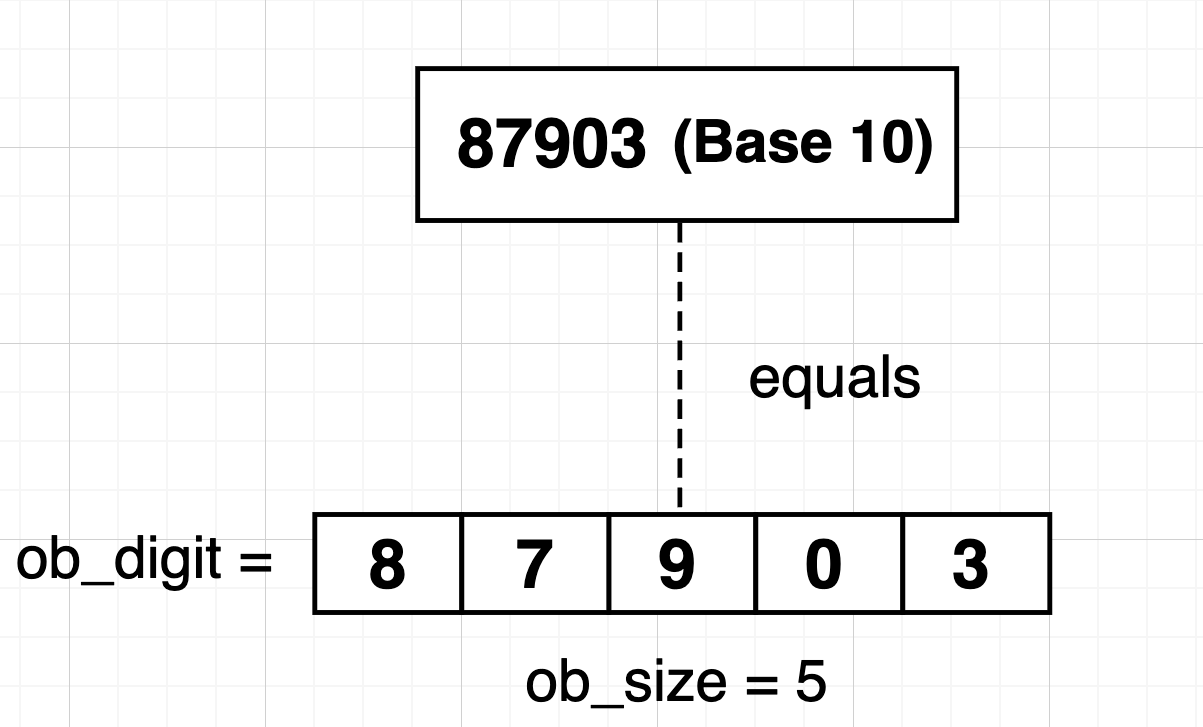
In variable ob_digit, which is an array of digit elements, every digit can hold a value from 0 to 2^32-1. If we store the values in base 10 (which will be 0 to 9), then only 4 bits will be used out of 32 bits which will lead to wastage of other bits. This approach is very inefficient as it leads to wastage of resources.

🙋🏻‍♂️ Then don’t we convert integers from base 10 to base 2^32 instead of 2^30?

The choice of base 2^30 is partly historical and partly practical. Earlier designs of arbitrary-precision arithmetic systems used bases that were convenient for the hardware and software of the time.

Smaller bases (like 2^15) would lead to more digits and thus more overhead in managing them, while larger bases (like 2^32) might not align as well with hardware optimizations and could lead to slower arithmetic operations.

Hope this helps!